This tutorial shows a very simple problem for HEAT FLOW coupled with MAGNETIC simulation.

Open FEMM and start new problem, menu > File > New .

Select Magnetics problem from the pop-up window, and set up magnetic problem as shown in Fig. 1 (example file can be downloaded at the bottom of this page). In this example there is single copper conductor next to a single magnetic block, both surrounded by a layer of non-magnetic (lossless) resin, and all of the geometry is placed in air.

Fig. 1. Magnetic problem

Once the magnetic problem is solved it is necessary to extract the power loss data from the regions of interest. Fig. 2 shows the sequence in which a given region can be selected, and the integral for Total Loss Density in W/m^3 can be extracted. This value will be used for the corresponding region in the Heat/Thermal model.

The values of loss density should be extracted for each region which contributes to power loss.

But all the lossless regions (such as air) will have zero loss by definition, so there is no need to process them.

In this example there are just two regions with loss:

• Copper bar = 706971 Watts/meter^3
• Magnetic bar = 77860.5 Watts/meter^3

Fig. 2. Use magnetic solution

Open FEMM and start new problem, menu > File > New .

Select Heat flow problem from the pop-up window, and set up the geometry as shown in Fig. 3 (example file can be downloaded at the bottom of this page).

NOTE: The geometry in the heat flow solver should correspond exactly to the geometry from the magnetic solver. To help with this process it is best to export the DXF file from the magnetic geometry by menu > File > Export DXF, and then importing this file into the heat solver by menu > File > Import DXF.

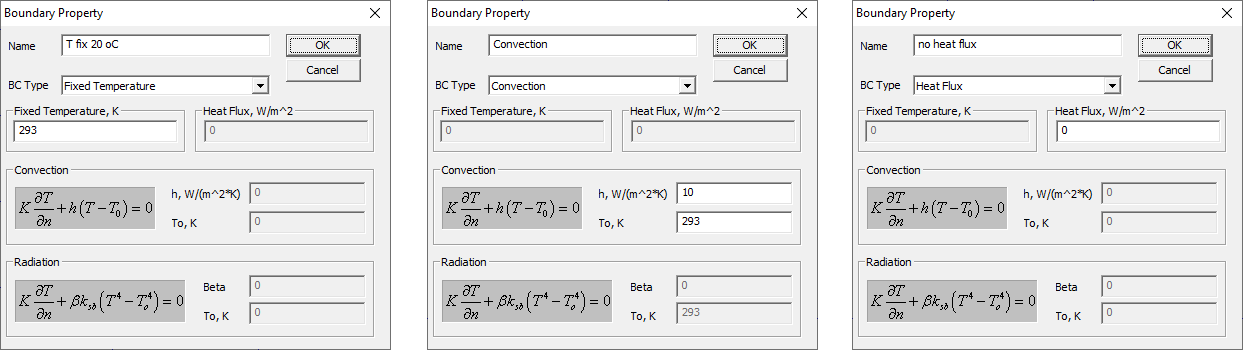
In the heat flow problem it is not necessary to create the “air box” so this can be removed, and the appropriate thermal boundary conditions can be assigned to all the edges of the geometry, as shown in Fig. 3 and as defined in Fig. 4.

Fig. 3. Heat flow geometry

Fig. 4. Heat flow boundary conditions

The heat sources can be assigned in several ways, also by forcing heat through boundary conditions. However, in this case we can use the values of Loss Density from the magnetic solver (as shown above in Fig. 2) and assigned them as Volume Heat Generation as shown in Fig. 5. If the value is set to zero in this field then it means that there is no heat produced within that material. Obviously also the thermal conductivity has to be set up correctly.

The Volumetric Heat Capacity is only important for transient problems, but it is a good practice to set it to correct values too.

Fig. 5. Heat sources in materials

The “steady state” problem assumes that the thermal conditions exist for infinitely long time. This is achieved by leaving the field “Previous Solution File Name” empty.

Fig. 6. Problem definition for steady state

In heat solution we can see that the regions which heat sources are hot, whereas other regions are cooled accordingly. The left vertical side is hotter because there is no heat flux (no cooling) assigned to that wall, whereas the right vertical side is cooler. The base is kept at 293 K as prescribed by the boundary assigned to that edge.

Fig. 7. Steady state heat solution

The transient heat calculations can be easily set in FEMM. This requires the following sequence:

1. Calculate the steady state “base” solution, for example with all the materials set to have zero power dissipation, which will make all the thermal solution to be at the ambient temperature everywhere.
2. Then use the name of the thermal solution file, and enter it in the problem definition in the field “Previous Solution File Name”.
3. The increment of time can be added in the field “Time Step”.
4. The transient solution can be performed with multiple step, by using the solution in the sequence: T0 → T1 → T2 etc.

Fig. 8. Transient heat solution